TANGRAM QUADRADO, OVAL E REDONDO

ATIVIDADE COM AS PEÇAS DO TANGRAM

01 – Responda as questões de acordo com a figura ao lado.

História do Tangram

Slide 2

Existem várias lendas sobre a origem deste jogo. Uma delas conta que um chinês deixou cair no chão um pedaço de espelho, de forma quadrada, o qual se quebrou em sete pedaços. Para sua surpresa, com os cacos do espelho, ele poderia dar origem a várias formas conhecidas como animais, plantas, pessoas, objetos, letras, números, figuras geométricas, entre outras.

Slide 3

Uma outra história do tangram diz que foi inventado por um homen enquanto tentava consertar os bocados quebrados de um azulejo de porcelana , o nome do home era Tan. Temos como primeira publicação do Tangram, na China, em 1813.Na Europa e na America durante o século XIX vemos um grande interesse por esse jogo.

Slide 4

Sam Loyd escreveu em 1903 "The Eighth Book of Tan-O oitavo livro de Tan". Afirmando que este quebra-cabeça fora inventado há 4.000 anos pelo Deus Tan. Mas o que realmente se sabe é que o tangram é um quebra-cabeça chinês e que hoje esse jogo milenar tem atraído muitos, tanto para entretenimento como para auxilio em conceitos matemáticos.

Slide 5

Luciana Gomes Ribeiro Embu - junho de 2009.

a) Quantas peças tem o Tangram?

b) Quantas peças são triangulares?

c) Quantas peças são quadriláteros?

d) Quantas peças são paralelogramos?



02 – Separe as peças do Tangram em grupos, de modo que em cada grupo todas as peças tenham o mesmo número de lados.

a) Em quantos grupos foi possível separar todas as peças?

b) Qual o nome que se dá às figuras de cada grupo?


03 – Brincando com as peças do Tangram, forme de acordo com as ordens da tabela.

Número de peças
Figuras
a) 2 Dois paralelogramos diferentes
b) 3 Um retângulo
c) 4 Dois paralelogramos diferentes
d) 5 Um trapézio

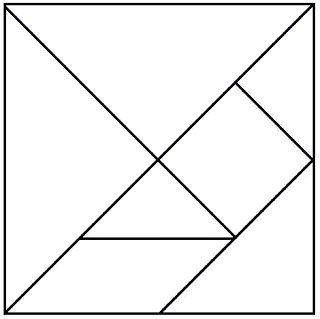
Tangram Conta-se que um dia, na China à 4000 anos, o Imperador Tan partiu o seu espelho quadrado quando o deixou cair ao chão. O espelho partiu-se em sete bocados. Tan, apesar de um pouco aborrecido com a perda do espelho, descobriu uma forma de se entreter, foi construindo figuras e mais figuras usando sempre as sete peças, sem as sobrepor. Assim se pensa ter aparecido o conhecido puzzle chinês, Tangram. Este puzzle também conhecido pela "placa das sete astúcias", possibilita a construção de diversas figuras partir de sete polígonos muito simples. Construção do Tangram Para obter um Tangram basta decompor um quadrado tal como mostra a figura: Com esta decomposição obtém-se sete polígonos, cinco triângulos, um quadrado e um paralelogramo. Esta construção foi feita de forma a que: AF=FB=ED DI=IH=GB O Tangram também pode ser obtido por simples dobragem de um quadrado de papel, como se pode afirmar na figura seguinte.

Composição de figuras usando o Tangram A decomposição e composição de figuras geométricas constituem uma actividade lúdica e permitem um melhor conhecimento das suas propriedades e das relações entre os seus elementos. De seguida são apresentadas algumas imagens construídas com as sete peças do Tangram.

FIGURAS COM AS PEÇAS DO TANGRAM Origem do tangram O tangram é um quebra-cabeça chinês, de origem milenar. Existem várias lendas sobre a origem deste jogo. Uma delas conta que um chinês deixou cair no chão um pedaço de espelho, de forma quadrada, o qual se quebrou em sete pedaços. Para sua surpresa, com os cacos do espelho, ele poderia dar origem a várias formas conhecidas como animais, plantas, pessoas, objetos, letras, números, figuras geométricas, entre outras. O objetivo deste jogo é utilizar as sete peças, sem sobreposição, para montar uma determinada figura. A referência mais antiga é de um painel em madeira, de 1780, de Utamaro com a imagem de duas senhoras chinesas a resolver um tangram. A mais antiga publicação com exercícios de tangram é do início do século XIX. Em chinês, o tangram é conhecido como Ch i ch iao t u, ou as Sete Peças Inteligentes. Existe uma enciclopédia do Tangram, escrita por uma mulher, na China, há mais de 100 anos, em seis volumes com 1700 problemas de Tangram. Vamos conhecer as peças que formam o tangram? O tangram é formado por: • 2 Triângulos grandes • 2 Triângulos pequenos • 1 Triângulo médio • 1 Quadrado • 1 Paralelogramo Veja algumas figuras que podem ser formadas com essas peças: Homem Coelho Cisne Barco Peixe Bruxa Gato Agora observe o tangram formado apenas com os triângulos grandes como ficaria: Como cabem 4 triângulos grandes dentro do quadrado, dizemos que cada um dos triângulos representa 1⁄4 do quadrado. Tangram oval Com o uso do tangram você pode trabalhar a identificação, comparação, descrição, classificação e desenho de formas geométricas planas., visualização e representação de figuras planas, exploração de transformações geométricas através de decomposição e composição de figuras, compreensão das propriedades das figuras geométricas planas, representação e resolução de problemas usando modelos geométricos. Esse trabalho permite o desenvolvimento de algumas habilidades tais como a visualização, percepção espacial, análise, desenho, escrita e construção. Se utilizado em terceiras e quartas séries pode envolver ainda noções de área e frações. Este é o Tangran Clássico: Tangran Oval O Tangram oval também conhecido por ovo mágico ou ovo de Colombo, tal como o Tangram clássico, propõe a construção de inúmeras figuras a partir de nove de peças com bordas curvas, e cujo objetivo era formar 95 figuras diferentes. Com o Tangran clássico formamos variadas figuras... Pessoas Animais Números Alfabeto Construção do Tangram 1.A partir de um Quadrado, ABCD, traça-se a sua diagonal DB, marca-se o seu ponto médio O e traça-se uma perpendicular a DB em O passando por A. 2.marca-se os pontos médios, M de DO e N de OB. 3.Marca-se os pontos médios, P de DC e Q de CB. Traça-se  o seguimento PQ e marca-se o seu ponto médio R  Exemplos      Esta atividade proporcionará a integração de varios conteúdos da geometria.Veja:       1.Figuras geometricas : sólidos geometricos, regiões planas, contornos;       2.vértice, aresta e face;       3.Retasparalelas e concorrentes;       4.Seguimentos e semi-retas;       5. Ângulos retos, agudo, obtuso e raso;       6.Ângulos complementares, suplementares e opostos pelo vértice;       7.Ângulos formados por retas paralelas cortadas por uma trans versal.       8.Etc...       Construa o tangram CORAÇÃO a partir de sua peça quadrada. materias necessários: lápis e borracha, esquadros, compasso. Atenção aos comandos:     1) Prolongue os seguimentos EC e EA totalizando 5 cm cada.     2) Abra o compasso em 2,5 cm e com o centro no vértice A, trace meia circunferência iniciando          no ponto E e achará o ponto F na outra extremidade da meia circunferência.     3) Faça o mesmo com o vértice C e achará o ponto H na outra extremidade da meia circunferência.     4) Com a régua nos vertices E e D trace  um seguimento de reta de 4 cm a partir do vértice D,          encontrando o ponto M.     5) Una os pontos H e M, M e F.     6) Trace um seguimento paralelo a DM partindo do vértice A e encontre o ponto P.     7) Prolongue os seguimentos DC até à circunferência e encontre o pontoR.     8) Faça o mesmo com seguimento DA e encontre o ponto S.     9) Trace um seguimento de reta perpendicular a AP partindo do vertice A e encontre o ponto X.                   Seu TANGRAM  de CORAÇÃO está pronto para ser recortado e trabalhado!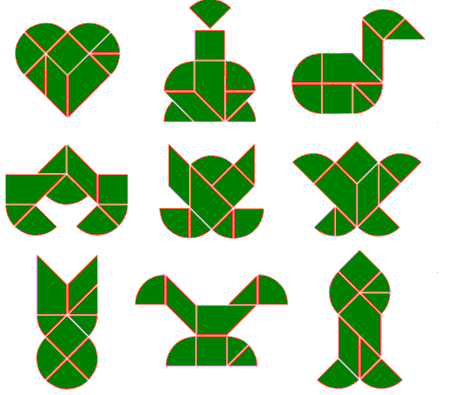

Conteúdos:- Múltiplos e divisores de um número natural;
- Números primos.

Objetivos:
- Saber reconhecer os múltiplos e divisores de um número natural;
- Entender o conceito de números primos;
- Resolver problemas procurando seus dados alguma regularidade que permita sua resolução, quando possível.

Habilidades:- Raciocínio lógico;
- Resolução de problemas;
- Integração.

Metodologia:
O desafio pode ser apresentado como atividade, em que o professor vai observar conhecimentos prévios em relação ao conteúdo proposto. Ou após a explicação como atividade de fixação.
Poderá ser resolvido em dupla, para que haja melhor integração entre os alunos.

JOGO

TANGRAM CORAÇÃO PARTIDO



Conteúdo:
- Polígonos.

Objetivos:- Identificação de diferente polígonos;
- Associação da Geometria como forma de desenvolver o gosto pela matemática.

Habilidades:- Criatividade;
- Análise;
- Observação;
- Classificação.

Metodologia:
O Tangram coração partido é um quebra-cabeça que possibilita as mais diversas atividades. Ele explora a coordenação motora, envolvendo relações entre parte de uma figura e sua totalidade, assim como sua composição.
É muito importante que os alunos tenham oportunidade de manipular as peças desse quebra-cabeça. Para isso, com as peças embaralhadas o professor deve orientá-los a remontar e depois criar algumas figuras usando todas as peças.